Pytorch tutorial (2)

Pytorch tutorial (2)

임의의 가중치로 그린 곡선과 실제 sin 곡선과 비교를 통해 가중치를 학습한 곡선을 비교해보겠습니다.

# 필요한 라이브러리 설치
import math
import toech
import matplotlib.pyplot as plt

x = torch.linspace(-math.pi, math.pi, 1000) # -pi부터 pi사이의 점 1000개 추출
y = torch.sin(x) # sin 곡선

-𝝅부터 𝝅까지 x값 1000개를 추출하고 정답비교를 위해 torch.sin()함수로 sin 곡선 y를 만들었습니다.

# 임의의 가중치
a = torch.randn(())
b = torch.randn(())
c = torch.randn(())
d = torch.randn(())

random한 값을 임의의 가중치 a,b,c,d 값으로 정의하고

y_rand = a * x**3 + b * x**2 + c * x + d

# 랜덤 가중치의 사인 곡선
plt.subplot(3, 1, 3)
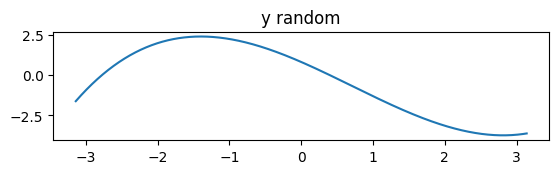
plt.title("y random")
plt.plot(x, y_rand)

랜덤한 가중치 값을 적용한 3차 곡선 y_rand는 아래와 같이 그려집니다.

이번에는 실제 sin 곡선인 y 값과 비교한 후 가중치를 학습해서 만든 함수 y_pred 값을 그려보겠습니다.

# 가중치 학습
learning_rate = 1e-6

for epoch in range(1000):
    y_pred = a * x**3 + b * x**2 + c * x + d
    
    loss = (y_pred - y).pow(2).sum().item() # 손실 MSE
    
    if epoch % 100 ==0:
        print(f"epoch : {epoch+1}, loss : {loss}")

    grad_y_pred = 2.0 * (y_pred - y)
    grad_a = (grad_y_pred * x ** 3).sum()
    grad_b = (grad_y_pred * x ** 2).sum()
    grad_c = (grad_y_pred * x).sum()
    grad_d = grad_y_pred.sum()

    # 가중치 업데이트
    a -= learning_rate * grad_a
    b -= learning_rate * grad_b
    c -= learning_rate * grad_c
    d -= learning_rate * grad_d

# output
epoch : 1, loss : 7937.68505859375
epoch : 101, loss : 3586.100830078125
epoch : 201, loss : 2924.1728515625
epoch : 301, loss : 2384.926025390625
epoch : 401, loss : 1945.4404296875
epoch : 501, loss : 1587.2352294921875
epoch : 601, loss : 1295.25390625
epoch : 701, loss : 1057.2337646484375
epoch : 801, loss : 863.1865234375
epoch : 901, loss : 704.974853515625z

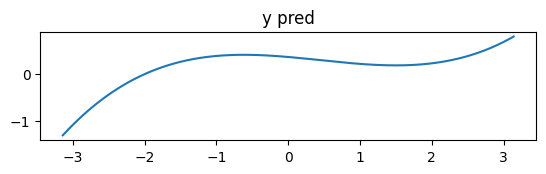
y_pred에 대한 곡선을 그리면 다음과 같습니다.

# 예측한 가중치의 사인 곡선
plt.subplot(3, 1, 2)
plt.title("y pred")
plt.plot(x, y_pred)

아래의 실제 sin 곡선과 비교해보면 가중치 학습을 통해서 y_pred 값이 sin 함수에 근사함을 알 수 있습니다.

# 실제 사인곡선
plt.subplot(3, 1, 1)
plt.title("y true")
plt.plot(x, y)

---

reference - 텐초의 파이토치 딥러닝 특강